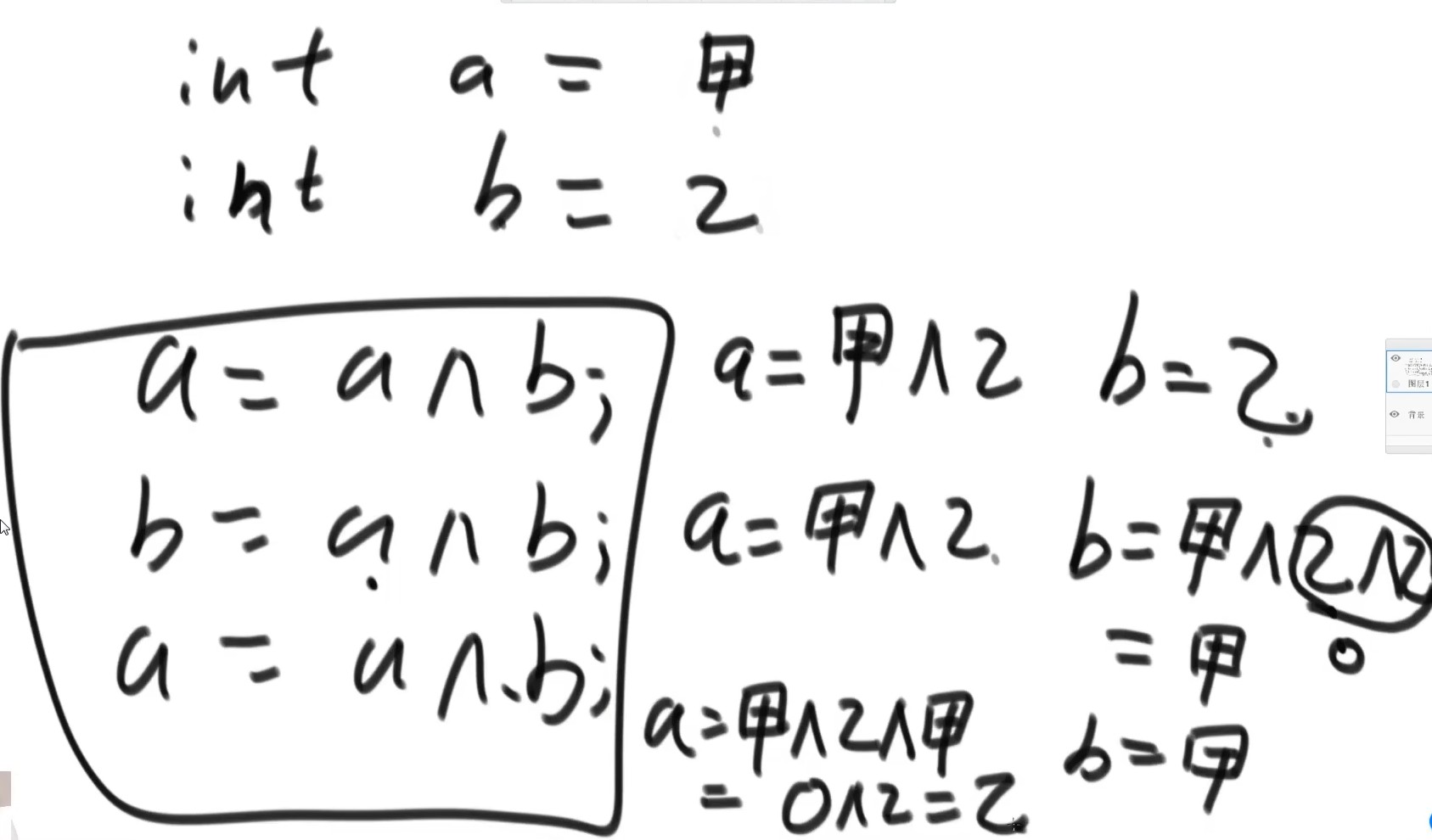计算机科学基础算法基本概念
Source
Edit
History

1. 认识复杂度和简单排序算法。1

第1节、时间复杂度

先从选择排序看起

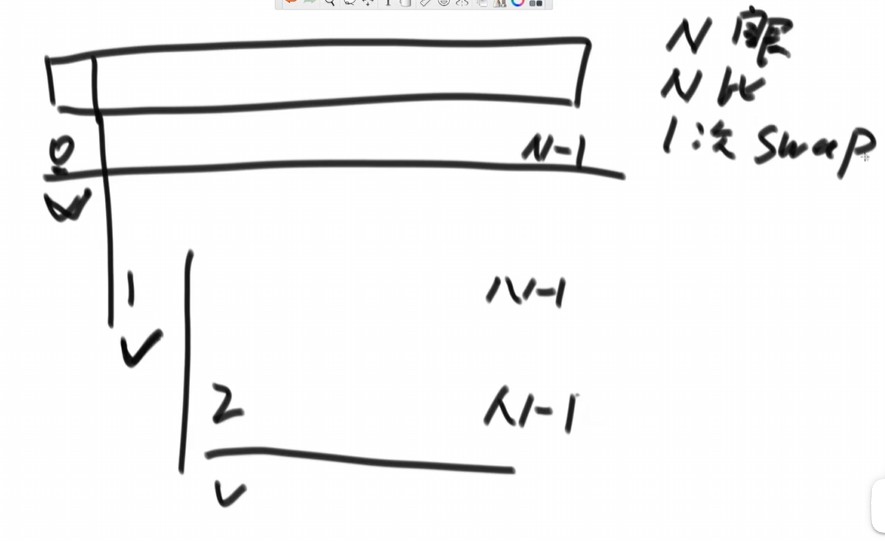
选择排序：从第1位到第N位。每一位分别与之后的所有数比较。比较小的树放在第i位。

Snipaste_2023-08-21_14-14-51

计算时间复杂度：

​ 每一个数分别看了后面的数：N次、N-1次、N-2次···1次。

​ 每个数分别比较了后面的数：N次、N-1次、N-2次···1次。

​ 每个数都交换了一次：1次。

所以可以得出时间复杂度：

​ 每个数看了： N+N-1+N-2+···+1。

​ 每一个数比较了： N+N-1+N-2+···+1。

​ 总共交换了N次。

全部相加可以得到： (N+1)*N + N 。

它是一个： 最高次项为二次的方程 aN^2+bN+c。

得到时间复复杂度为 O(N^2) 读作：big o N^2。

第2节、额外空间复杂度（选择排序）

这里我们也可以从选择排序看起

下面我们给出选择排序的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
namespace LeetCode_Learn
{
    public class Part01_SelectionSort
    {
        public static int[] Sort(int[] arr)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr;

            for (int i = 0; i < arr.Length; i++)
            {
                int minIndex = i;
                for (int j = i + 1; j < arr.Length; j++)
                {
                    minIndex = arr[j] < arr[minIndex] ? j : minIndex;
                }
                Swap(arr, i, minIndex);
            }

            return arr;
        }

        private static void Swap(int[] arr, int index1, int index2)
        {
            int temp = arr[index1];
            arr[index1] = arr[index2];
            arr[index2] = temp;
        }
    }
}

在遍历每个数字的时候，我们会声明一个temp作为最小的最小的index。每次去每次循环完之后会释放掉这个temp，所以这里我们只用到了开辟了一个变量。也就是额外空间复杂度为O(1) 。

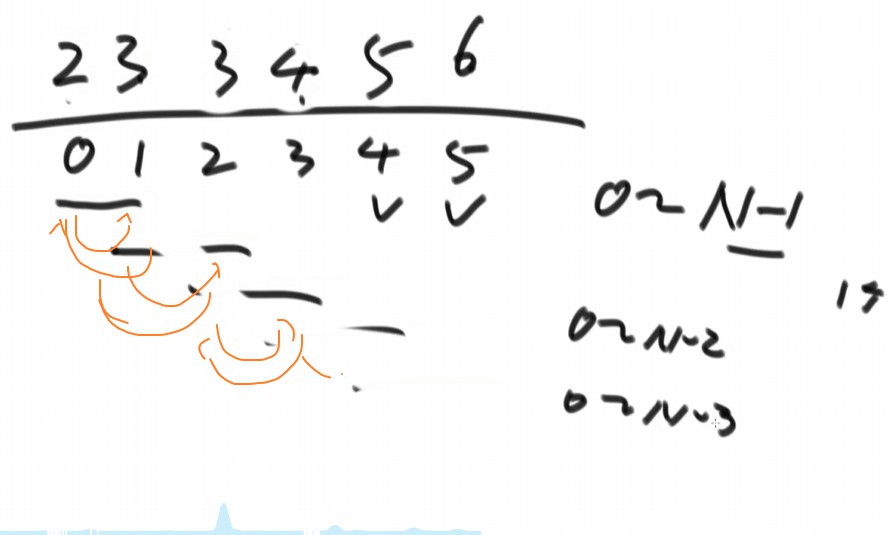
第3节、冒泡排序

冒泡排序：遍历每个数，其左边边的数做以下操作: 如果右边的数大于左边的数则交换。

Snipaste_2023-08-21_14-16-01

下面给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
namespace LeetCode_Learn
{
    public class Part02_BubbleSort
    {
        public static int[] Sort(int[] arr)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr;

            for (int i = arr.Length - 1; i >= 0; i--)
            {
                for (int j = 0; j < i; j++)
                {
                    if (arr[j] > arr[j + 1])
                    {
                        Swap(arr, j, j + 1);
                    }
                }
            }

            return arr;
        }

        private static void Swap(int[] arr, int index1, int index2)
        {
            arr[index1] = arr[index1] ^ arr[index2];
            arr[index2] = arr[index1] ^ arr[index2];
            arr[index1] = arr[index1] ^ arr[index2];
        }
    }
}

这里用到异或运算进行。进行交换操作。

Snipaste_2023-08-21_13-16-55

第4节、异或运算

下面给出异或运算的一些规律：

  1. 0^N = N。

  2. N^N = 0。

  3. 符合交换律和结合律。

  4. 异或运算与顺序无关，可以调换顺序。

  5. 注意事项:如果要进行用异或运算进行交换操作，请注意a和b指向的内存空间不能为同一个。因为N^N=0。

下面给出一道异或运算的练习题：

​ 给出一个整形数组 int[] arr

​ 第1问：这个数组中仅有一种数出现奇数次，其他数都是偶数次。求这个基数是多少？

​ 第2问：这个数组中仅有二种数出现奇数次。其他数都是都是偶数次。求这两个奇数分别是多少？

​ 第1题，题解：

​ 定义eor = 0,用eor 异或每一个数得到的数一定是出现奇数次的数。因为出现偶数次的数异或为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
namespace LeetCode_Learn
{
    public class Part03_GetOneOddNumber
    {
        public static int Get(int[] arr)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr[0];

            int eor = 0;
            for (int i = 0; i < arr.Length; i++)
            {
                eor ^= arr[i];
            }

            return eor;
        }
    }
}

​ 第2题，题解：

​ 同上题用eor异或每一个数。得到的eor为 a异或b。 a和b是那两个出现奇数次的数。然后我们在定义一个变量_eor = 0。因为a和b不为同一个数，所以 eor不等于0。所以我们一定可以在eor中找到一位为1。这里我们用一个算法来找到最右侧的1:

​ 算法为 rightOne = eor & (~eor+1) 。

​ a和b在rightOne这一位，一定有一位是1，有一位是0。这里我们将数组分为两种类型。种是对应位为1，一种是对应位为0。a和b肯定只占一种类型。然后我们遍历对应位为1的数。用_eor异或这些数。我们一定可以得到a或者b。然后我们再用得到的这个数，来异或eor。这样我们就得到了这两个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
namespace LeetCode_Learn
{
    public class Part04_GetTwoOddNumber
    {
        public static int[] Get(int[] arr)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr;

            int eor = 0;

            for (int i = 0; i < arr.Length; i++)
            {
                eor ^= arr[i];
            }

            int _eor = 0;
            int rightOne = eor & (~eor + 1);

            for (int i = 0; i < arr.Length; i++)
            {
                if ((arr[i] & rightOne) == 0)
                {
                    _eor ^= arr[i];
                }
            }
            int a = eor ^ _eor;
            int b = eor ^ a;
            return new int[] { a, b };
        }
    }
}

第5节、插入排序

遍历每个数使其左边的数变成成有序态。遍历左边的数如果左边的时候大于右边，那就交换。

插入排序的时间复杂度。最差复杂度为O(N^2)。最好是复杂度为O(N)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/// <summary>
/// 插入排序
/// </summary>
public class Part05_InsertSort
{
    public static int[] Sort(int[] arr)
    {
        if (arr == null)
            throw new ArgumentNullException("arr不可为空!");
        if (arr.Length < 2)
            return arr;

        for (int i = 1; i < arr.Length; i++)
        {
            for (int j = i - 1; j >= 0; j--)
            {
                if (arr[j] > arr[j + 1])
                {
                    Swap(arr, j, j + 1);
                }
            }
        }

        return arr;
    }

    private static void Swap(int[] arr, int index1, int index2)
    {
        arr[index1] = arr[index1] ^ arr[index2];
        arr[index2] = arr[index1] ^ arr[index2];
        arr[index1] = arr[index1] ^ arr[index2];
    }
}

第6节、二分法

  1. 有序数组中的二分法。在有序数组中的一个数是否存在？时间复杂度为big，log2为底的N次方。

  2. 有序数组中找大于等于某个数最左侧的位置。与上题相同,不过要二分到最左侧的位置。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    public class Part06_BSOne
    {
        public static int Get(int[] arr, int num)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr[0];

            return binaryFindNum(arr,0, arr.Length - 1,num);
        }

        public static int binaryFindNum(int[] arr, int left, int right, int num)
        {
            if (left > right)//递归结束
                return -1;
            int mid = (left + right) / 2;
            int midVal = arr[mid];
            if (num > midVal)
                return binaryFindNum(arr, mid + 1, right, num);//向右递归
            else if (num < midVal)
                return binaryFindNum(arr, left, mid - 1, num);//向左递归
            else
                return mid;
        }
    }

  3. 局部最小问题。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    public class Part06_BSOneLeftNear
    {
        public static int Get(int[] arr, int num)
        {
            if (arr == null)
                throw new ArgumentNullException("arr不可为空!");
            if (arr.Length < 2)
                return arr[0];

            return binary(arr, 0, arr.Length - 1, num);
        }

        public static int binary(int[] arr, int left, int right, int num)
        {
            if (left > right)//递归结束
                return -1;
            int mid = (left + right) / 2;
            int midVal = arr[mid];
            //如果当前中间值>=num且左边元素也>=num,则向左递归
            if (mid - 1 >= 0 && midVal >= num && arr[mid - 1] >= num)
                return binary(arr, left, mid - 1, num);//向左递归
                                                       //如果当前中间值>=num但左边元素<num,则直接返回该中间值
            else if (mid - 1 >= 0 && midVal >= num && arr[mid - 1] < num)
                return mid;
            //其他情况向右递归
            else
                return binary(arr, mid + 1, right, num);//向右递归
        }

    }

第7节、对数器

实现一个简单的C#对数器,实现排序算法对比

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public class Compare
{
    public static void DO(int number, Action<int[]> CustomSort, int length, int min, int max)
    {
        if (number == 0) return;

        for (int i = 0; i < number; i++)
        {
            DO(CustomSort, length, min, max);
        }
    }

    static bool DO(Action<int[]> CustomSort, int length, int min, int max)
    {
        int[] arr = new int[length];
        RandomArr(arr, length, min, max);

        int[] arr1 = new int[length];
        Array.Copy(arr, arr1, length);

        int[] arr2 = new int[length];
        Array.Copy(arr, arr2, length);

        Array.Sort(arr1);
        CustomSort(arr2);

        if (!Do(arr1, arr2, length))
        {
            Console.ForegroundColor = ConsoleColor.Red;
            Console.WriteLine($"错误样本{string.Join(", ", arr)}");
            Console.WriteLine($"错误样本排序: {string.Join(", ", arr2)}");
            Console.WriteLine("\n");
            return false;
        }
        else
        {
            Console.ForegroundColor = ConsoleColor.Green;
            Console.WriteLine($"正确样本{string.Join(", ", arr)}");
            Console.WriteLine($"正确样本排序{string.Join(", ", arr2)}");
            Console.WriteLine("\n");
        };

        Console.ForegroundColor = ConsoleColor.White;
        return true;
    }

    static bool Do(int[] arr1, int[] arr2, int length)
    {
        bool right = true;
        for (int i = 0; i < length; i++)
        {
            if (arr1[i] == arr2[i])
            {

            }
            else
            {
                right = false;
            };
        }
        return right;
    }

    static void RandomArr(int[] arr, int length, int min, int max)
    {
        Random rand = new Random();
        for (int i = 0; i < length; i++)
        {
            arr[i] = rand.Next(min, max);
        }
    }
}