物理
, ,
Source
Edit
History

分离轴算法

Reference

翻译自：Separating Axis Theorem (SAT) Explanation – sevenson.com.au

Separating Axis Theorem (SAT) Explanation

Separating Axis Theorem (SAT) is a technique for calculating collisions between convex polygons.
分离轴定理 （SAT） 是一种计算凸多边形之间碰撞的技术。

I’m by no means an expert on it, but after the need arose for me to do some collision detection I did a pile of reading and finally got it working in ActionScript 3.
我绝不是这方面的专家，但是在我需要做一些碰撞检测之后，我做了大量的阅读，最终让它在 ActionScript 3 中工作。

I thought I would share what I learned in the hope others wouldn’t suffer so much 🙂
我想我会分享我所学到的东西，希望其他人不会遭受那么多🙂痛苦

When I found myself in a need to calculate collisions between polygons in flash, I came across a method known as Separating Axis Theorem (SAT). The only problem I had was that I really struggled to get a grasp on it.
当我发现自己需要在 Flash 中计算多边形之间的碰撞时，我遇到了一种称为分离轴定理 （SAT） 的方法。我唯一的问题是我真的很难掌握它。

After a lot of reading about collision detection, and looking at code samples, it all finally clicked.
在阅读了大量有关碰撞检测的内容并查看了代码示例之后，它终于点击了。

To help out the other non-maths minded people I thought I would write this quick explanation to run through the basic principles of how it works. I’ve also included a demo using SAT collision detection, as well as some ActionScript 3 classes you can download and use.
为了帮助其他不懂数学的人，我想我会写这个简短的解释来介绍它如何工作的基本原理。我还提供了一个使用 SAT 冲突检测的演示，以及一些您可以下载和使用的 ActionScript 3 类。

Note: SAT does require a bit of work with vector math, so it may be a good idea to brush up on your vectors before getting too far into SAT.
注意：SAT 确实需要一些矢量数学方面的工作，因此在深入 SAT 之前复习一下矢量可能是个好主意。

这里有一个DEMO可以在网页上面运行的碰撞检测实例

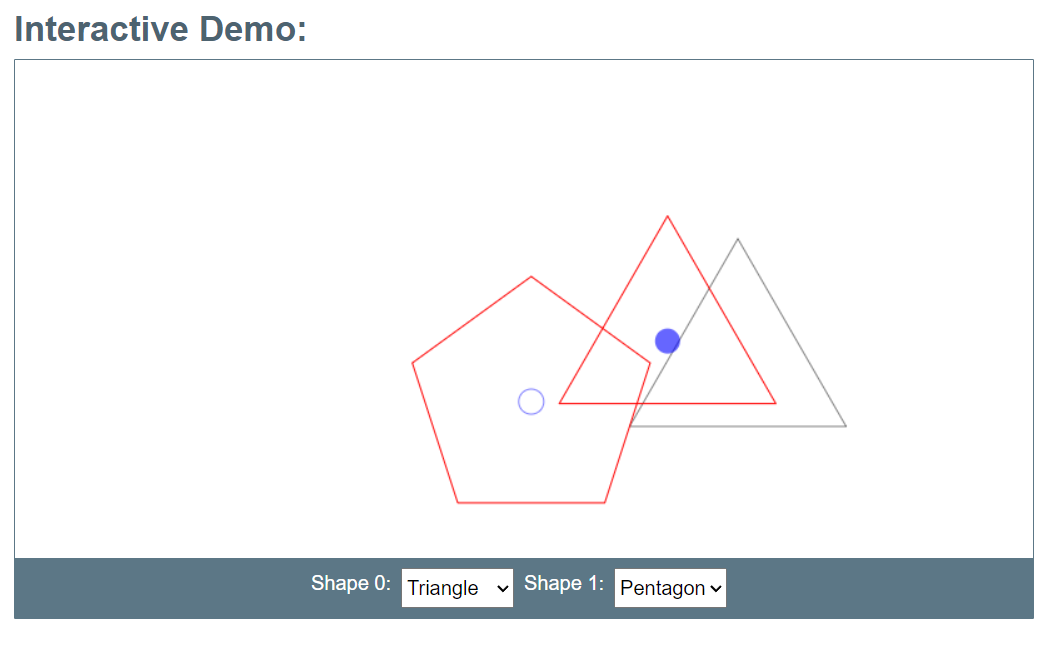
Use your mouse to drag the shapes around. Whilst dragging, use the arrow keys to change the scale and rotation of the shapes. When the two shapes collide they will change colour (red) and show a possible reaction (grey).
使用鼠标拖动形状。拖动时，使用箭头键更改形状的比例和旋转。当两个形状碰撞时，它们会改变颜色（红色）并显示可能的反应（灰色）。

The quick rundown 快速纲要

Basically, the goal of SAT (and every other collision detection) is to test and see if is a gap between two shapes. The method that SAT uses is what makes it unique.
基本上，SAT（以及所有其他碰撞检测）的目标是测试并查看两个形状之间是否存在间隙。SAT 使用的方法使其独一无二。

The best analogy I have heard for SAT technique is like this:
我听说过的关于SAT技术的最好的类比是这样的：

Imagine taking a torch and shining it on the two shapes you are testing from different angles. What sort of shadows would it cast on the wall behind it?
想象一下，拿起手电筒，从不同的角度照射你正在测试的两个形状。它会在它后面的墙上投下什么样的阴影？

If you work your way around the shapes and never find a gap in the shadows then the objects must be touching. If you find a gap, then they are clearly not touching.
如果你在形状周围工作，却从未在阴影中找到间隙，那么物体一定是接触的。如果你发现一个缝隙，那么它们显然没有接触。

From a programming point of view it would be too intensive to check every possible angle. Luckily, due to the nature of the polygons, there is only a few key angles you need to check.
从编程的角度来看，检查每个可能的角度都太密集了。幸运的是，由于多边形的性质，您只需要检查几个关键角度。

The angles you need to check are the same as the sides of the polygons. This means that the maximum number of angles to check is the sum of the number of sides the two shapes you are testing have. Eg. Two pentagons would require ten angles to be checked.
您需要检查的角度与多边形的边相同。这意味着要检查的最大角度数是要测试的两个形状的边数之和。例如。两个五边形需要十个角度才能检查。

So how do you make it work in code?

那么，如何让它在代码中工作呢？

It’s a simple but repetitive method, so here is a very basic step by step.
这是一个简单但重复的方法，所以这是一个非常基本的步骤。

Please Note: that the code samples are just a very rough guide as to how it could be done. For a more complete working sample, check out the download section
请注意：代码示例只是一个非常粗略的指南，说明如何做到这一点。有关更完整的工作示例，请查看下载部分

Step 1. Take one side from one of the polygons you are testing and find the normal (perpendicular) vector from it. This will be the ‘axis’. It needs to be a unit vector, so when you calculate it, be sure to normalize it.
步骤 1。从您正在测试的多边形之一中选取一条边，并从中找到法向（垂直）向量。这将是“轴”。它必须是一个单位向量，所以当你计算它时，一定要把它归一化。

Something a bit like: 有点像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// points / verts in the geometry.  Make sure they are in  ❗ 🔄
let vertices = [ {x:1, y:1}, {x:1, y:-1}, {x:-1, y:-1}, {x:-1, y:1} ];
// get the perpendicular axis - you would need to loop over these... ❗ 🔄
let axis = { 
   x: -(vertices[1].y - vertices[0].y), 
   y: vertices[1].x - vertices[0].x
}
// be sure to normalize the axis by making it length to 1. You can do that with something like ❗ 🔄
let magnitude = Math.sqrt(Math.pow(axis.x,2), Math.pow(axis.y, 2));
if (magnitude != 0)
{
   axis.x *= 1 / magnitude;
   axis.y *= 1 / magnitude;
}

Step 2. Loop through every point on the first polygon and project it onto the axis. (Keep track of the highest and lowest values found for this polygon) 
第2步。遍历第一个多边形上的每个点，并将其投影到轴上。（跟踪找到的此多边形的最高值和最低值）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
  // helper method for calculating the dot product of a vector  
  //用于计算向量的点积的辅助方法
  vectorDotProduct(pt1, pt2)
  {
     return (pt1.x * pt2.x) + (pt1.y * pt2.y);
  }
  // verts and axis from earlier...  
  //前面的顶点和轴...
  vertices = [ {x:1, y:1}, {x:1, y:-1}, {x:-1, y:-1}, {x:-1, y:1} ];    
  axis = {x:1, y: 0}  
  // get an initial min/max value.  you will need the min max for both shapes  
//获取初始最小值/最大值。 您将需要两种形状的最小最大值
  let p1min = vectorDotProduct(axis, vertices[0]);
  let p1max = min;
  // loop over all the other verts to complete the range  
//在所有其他顶点上循环以完成范围
  for (let i =1; i < verts.length; i++)
  { 
     let dot = vertices[i];
     p1min = Math.min(p1min , dot);
     p1max = Math.max(p1max , dot);
  }

Step 3. Do the same for the second polygon. 
第 3 步。对第二个多边形执行相同的操作。
Now you will have both sets of vertices projected onto the axis, which is good, but they will probably be overlapping at this point because we haven’t taken into consideration the distance between the two objects. (I forgot about this step until I rewrote the code, hence the picture doesn’t show it…) You can correct for this spacing issue by projecting the distance between the shapes onto the same axis, then adding it to one of the shapes projection. Something kinda like this:
现在，您将把两组顶点投影到轴上，这很好，但是它们此时可能会重叠，因为我们没有考虑两个对象之间的距离。（在我重写代码之前，我忘记了这一步，因此图片没有显示它……您可以通过将形状之间的距离投影到同一轴上，然后将其添加到其中一个形状投影来纠正此间距问题。有点像这样：

1
2
3
4
5
6
7
8
9
10
11
  // vector offset between the two shapes  
  //两个形状之间的矢量偏移
  let vOffset = { polygon1.x - polygon2.x, polygon1.y - polygon2.y };
  // project that onto the same axis as just used  
//将其投影到刚才使用的同一轴上
  let sOffset = vectorDotProduct(axis, vOffset);
  //that will give you a scaler value that you can add to the min/max of one of the polygons from earlier  
//这将为您提供一个缩放器值，您可以将其添加到前面其中一个多边形的最小值/最大值中
  p1min += sOffset;
  p1max += sOffset;

Step 4. Check the values you found and see if they overlap.
第 4 步。检查您找到的值，看看它们是否重叠。

If you find a gap between the two ‘shadows’ you have projected onto the axis then the shapes must not intersect. However, if there is no gap, then they might be touching and you have to keep checking until you have gone through every side of both polygons. If you get through them all without finding a gap then they collide.
如果发现投影到轴上的两个“阴影”之间有间隙，则形状不得相交。但是，如果没有间隙，那么它们可能会接触，您必须继续检查，直到您穿过两个多边形的每一条边。如果你穿过它们而没有找到缝隙，那么它们就会碰撞。

1
2
3
4
5
6
7
8
   //quick overlap test of the min and max from both polygons  
//两个多边形的最小值和最大值的快速重叠测试
  if ( (p1min - p2max > 0) || p2min - p1max > 0)  )
  {
     // there is a gap - bail  
  //有一个缺口
     return null;
  }

That’s basically it. 基本上就是这样。

As an added bonus, if you keep track of which axis has the smallest shadow overlap (and how much of an overlap that was) then you can apply that value to the shapes to separate them.
作为额外的奖励，如果您跟踪哪个轴具有最小的阴影重叠（以及重叠的程度），则可以将该值应用于形状以分隔它们。

What about circles? 圈子呢？

Testing a circle against a polygon in SAT is a little bit strange but it can be done.
在 SAT 中针对多边形测试圆有点奇怪，但可以做到。

The main thing to note is that a circle does not have any sides so there is no obvious axis that you can test against. There is one ‘not so obvious’ axis you do need to test however. This is the axis that runs from the centre of the circle to the closest vertex on the polygon.
需要注意的主要事情是，圆没有任何边，因此没有明显的轴可以测试。但是，您确实需要测试一个“不太明显”的轴。这是从圆心到多边形上最近顶点的轴。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
  // presume with have some info  
//假设有一些信息
  vertices = [ {x:1, y:1}, {x:1, y:-1}, {x:-1, y:-1}, {x:-1, y:1} ];
  polygonPos = { x:0, y: 0}
  circlePos = { x: 5, y:1}
  circleRadiuis = 4;
  // find the closest by doing a distance check  
//通过进行距离检查找到最近的
  let minDist = Number.MAX_VALUE;
  let closestDelta = null;
  let axis = null;
  for (let vert in vertices)
  {
     // make sure you are using the vert in the same space... this will depend on how you have the data set up  
//确保您在同一空间中使用 VERT...这取决于您如何设置数据
     let worldVert = { x: polygonPos.x + vert.x, y: polygonPos.y + vert.y }
     // delta between the circle and this vert in world space.  
//世界空间中圆圈和这个顶点之间的三角洲。
     let delta= { x: worldVert.x - circlePos.x, y: worldVert.y - circlePos.y }
     // use pythagoras theorem to get the distance - you can skip the sqrt because we don't need the true distance in this check  
//使用毕达哥拉斯定理来计算距离 - 您可以跳过 sqrt，因为在此检查中我们不需要真实距离
     let dist = Math.pow(delta.x, 2) +  Math.pow(delta.y, 2));
     if (dist < minDist)
     {
     minDist = dist;
     closestDelta = delta;
     }
  }
  // you can now convert the closest delta into a unit vector axis  
//您现在可以将最近的增量转换为单位矢量轴
  let magnitude = Math.sqrt(Math.pow(closestDelta.x,2), Math.pow(closestDelta.y, 2));
  if (magnitude != 0)
  {
     axis.x = closestDelta.x * (1 / magnitude);
     axis.y = closestDelta.x * (1 / magnitude);
  }

After that it is just a matter of going through the usual routine of looping through every axis on the other polygon and checking for overlaps.
之后，只需完成常规例程，即可遍历另一个多边形上的每个轴并检查重叠。

Oh, and in case you are wondering how to project a circle onto the axis, you simply project the centre point of the circle and then add and subtract the radius.
哦，如果你想知道如何将圆投影到轴上，你只需投影圆的中心点，然后加减半径。

1
2
3
4
5
6
7
8
9
10
11
  // props from earlier 早期的道具
  // axis = {x:1, y: 0}  
  // circleCenter = {x:5, y:1 }  
  // project the center 项目中心
  let temp = vectorDotProduct(axis, circleCenter );
  // calc the range using the radius  
//使用半径计算范围
  let circleMin = temp - circleRadius;
  let circleMax = temp + circleRadius;
  // Now use this range to do the overlap test described earlier...  
  //现在使用此范围进行前面描述的重叠测试...

Pros and Cons 优点和缺点

Like all collision detection techniques, SAT has it’s pro’s and cons. Here is a quick rundown of some of them:
像所有碰撞检测技术一样，SAT也有其优点和缺点。以下是其中一些的简要介绍：

Pros

  • It is fast - It uses pretty basic vector math and you can bail out of a test as soon as a gap is detected, eliminating unnecessary calculations.
    它速度很快 - 它使用非常基本的向量数学，一旦检测到差距，您就可以退出测试，从而消除不必要的计算。
  • It is accurate - at least as far as I can tell.
    这是准确的——至少据我所知。

Cons

  • It only works with Convex polygons - complex shapes are out unless you build them out of smaller convex shapes, and then test each individual shape.
    它仅适用于凸多边形 - 除非您从较小的凸形中构建它们，然后测试每个单独的形状，否则复杂形状将被排除在外。
  • It doesn’t tell you which sides are touching - only how far they are overlapping and the shortest distance to separate them.
    它不会告诉你哪些方面是接触的，只是告诉你它们重叠的距离和分开它们的最短距离。

There is probably a bunch more but these were the main ones I could think of.
可能还有很多，但这些是我能想到的主要的。

Conclusion

I hope that this has helped to shed some light on the separating axis theorem. I’ve tried to keep it as simple as possible without shedding too much information. (I’m by no means an expert in maths so I apologise if I left anything out)
我希望这有助于阐明分离轴定理。我试图让它尽可能简单，而不会泄露太多信息。（我绝不是数学专家，所以如果我遗漏了什么，我深表歉意）

Here are a few links to other pages that helped me understand SAT collision detection.
以下是一些指向其他页面的链接，这些页面帮助我了解了 SAT 碰撞检测。

  • harverycartel.org - more detailed descriptions and some cool interactive examples. I learnt a lot from this page.
    harverycartel.org - 更详细的描述和一些很酷的交互式示例。我从这个页面学到了很多东西。
  • GPWiki.org- good SAT explanation and sample code - I used this as a basis for creating my own code.
    GPWiki.org - 良好的 SAT 解释和示例代码 - 我以此为基础创建自己的代码。
  • Tony Pa - Vector tutorials - Good resource for learning about Vectors
    Tony Pa - Vector 教程 - 学习 Vectors 的好资源
  • GameDev.net forum - a SAT collision system a member created - gave me some ideas on how to calculate reactions, etc.
    GameDev.net 论坛 - 一个成员创建的SAT碰撞系统 - 给了我一些关于如何计算反应等的想法。

Download:

If you want to see the code for my interactive demo, you can grab them from my SAT_JS GitHub Repo. It is in no way optimised but should serve as a good example of the above explanation.
如果你想查看我的交互式演示的代码，你可以从我的 SAT_JS GitHub Repo 中获取它们。它绝不是优化的，但应该作为上述解释的一个很好的例子。
(The original AS3 version is also available is you are so inclined)
（原始的 AS3 版本也可用，您愿意）

Basically, you create two shapes from the (SATPolygon or SATCircle classes) and then test them with the static ‘SAT.test()’ method. If they touch then a ‘CollisionInfo’ object will be returned. If they don’t touch then it will return ‘null’. The CollisionInfo object has a bunch of information about the collision that can be used to separate the two objects, etc.
基本上，您从（SATPolygon 或 SATCircle 类）创建两个形状，然后使用静态的“SAT.test（）”方法测试它们。如果它们接触，则将返回“CollisionInfo”对象。如果他们不接触，那么它将返回“null”。CollisionInfo 对象有一堆关于碰撞的信息，可用于分隔两个对象等。

The SATDemo class contains all the logic for creating the demo shown earlier in this post.
SATDemo 类包含用于创建本文前面所示的演示的所有逻辑。