Reference
Unity 几何着色器 - 世纪末の魔术师 - 博客园 (cnblogs.com)
几何着色器(Geometry Shader)的基础介绍以及简单示例 - 知乎 (zhihu.com)
几何着色器 - 知乎 (zhihu.com)
OpenGL - 教程 - 高阶 - 几何着色器 - 知乎 (zhihu.com)
什么是几何着色器
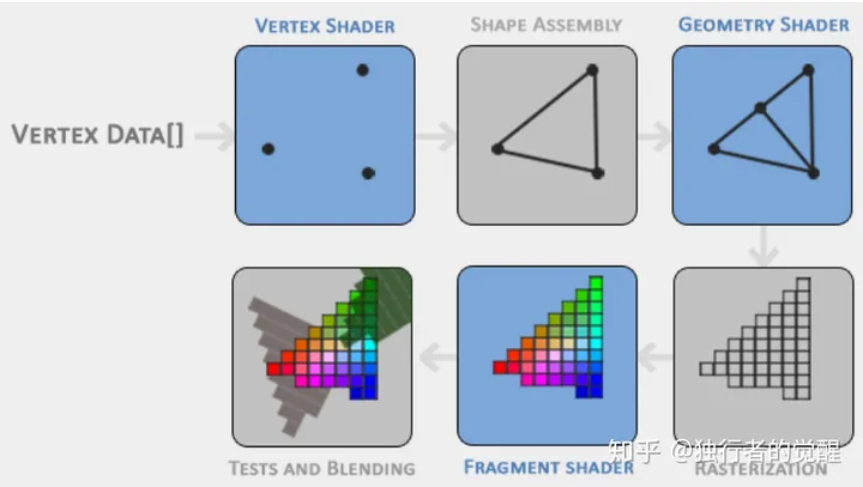
顶点着色器以顶点数据作为输入数据,而几何着色器则以完整的图元Primitive作为输入数据。例如,以三角形的三个顶点作为输入,然后输出对应的图元。与顶点着色器不能销毁或创建顶点不同,几何着色器的主要亮点就是可以创建或销毁几何图元,此功能让GPU可以实现一些有趣的效果。
– 几何着色器 - 知乎 (zhihu.com)
几何着色器的使用
为了理解几何着色器是如何工作的,我们首先来看一个例子:

几何着色器的GLSL
- 输入类型 (Input Types)
layout(points) in;
我们知道几何着色器的输入是图元,那么到底可以处理那些图元呢?可用的图元类型如下所示(括号里面的数字表示所需要的顶点数目):
- points-GL_POINTS (1)
- lines-GL_LINES, GL_LINE_STRIP, GL_LINE_LIST (2)
- lines_adjacency-GL_LINES_ADJACENCY, GL_LINE_STRIP_ADJACENCY (4)
- triangles-GL_TRIANGLES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN(3)
- triangles_adjacency-GL_TRIANGLES_ADJACENCY, GL_TRIANGLE_STRIP_ADJACENCY (6)
如果我们使用glDrawArrays(GL_POINTS, 0, 4)命令来绘制点图元,那么我们需要传入points参数。
- 输出类型 (Output Types)
layout(line_strip, max_vertices = 2) out;
下一行代码展示的是几何着色器的输出。几何着色器最有意思的地方在于:输出图元类型跟输入图元类型完全不同,而且输出图元的数量跟输入图元数量也没有关系。括号里面的参数分别表示:输出图元类型和图元最大顶点数。输出图元的类型可以是下面几种:
- points
- line_strip
- triangle_strip
我们可以发现这三种类型的输出图元可以覆盖所有可能的图元类型,比如,我们可以用3个顶点的triangle_strip来输出一个普通的triangle。
几何着色器的输出要求我们最大输出顶点数目,当EmitVertex()的数量超出该值时,OpenGL将不会绘制更多的顶点。
- 顶点输入 (Vertex Input)
我们在顶点着色器使用的gl_Position变量其实位于gl_in数组中,该数组的数据成员如下所示:
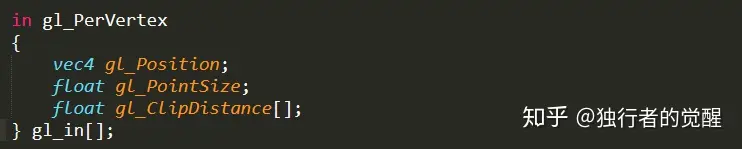
gl_in数组
需要注意的是,由于几何着色器的输入是图元的所有顶点,所以这里将gl_in定义为数组。
- 顶点输出 (Vertex Output)
我们使用EmitVertex()和EndPrimitive()两个函数来产生图元。每当我们调用一次EmitVertex()函数时,会将顶点加入到当前的图元;当所有顶点都加入到图元后,我们可以通过EndPrimitive()函数来产生图元。我们需要注意,当我们重复调用EndPrimitive()时,可以生成多个同样的图元。
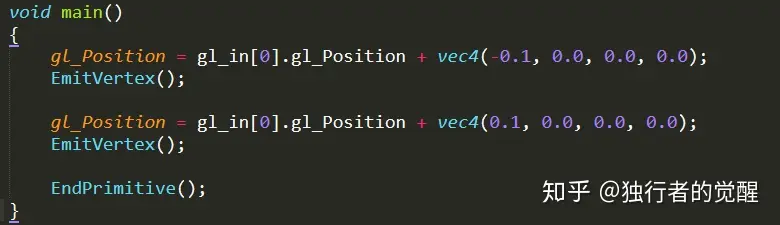
通过执行该几何着色器,我们得到下面的输出,我们发现GPU的输出是一条线段,而不是顶点。

利用几何着色器得到的输出
我们可以在顶点着色器中输入颜色分量来控制几何着色器中每个顶点的颜色。我们发现其实几何着色器对颜色的处理和片段着色器差不多,只不多这里的输入是颜色数组,因为输入图元的每个顶点都对应一个自己的颜色属性。
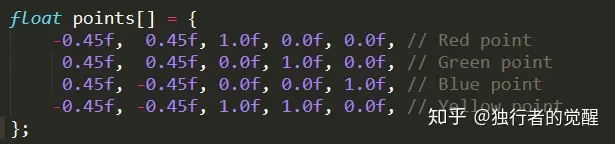
顶点属性包括了颜色信息
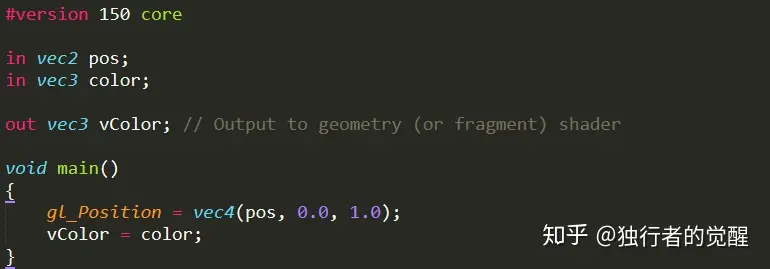
顶点着色器
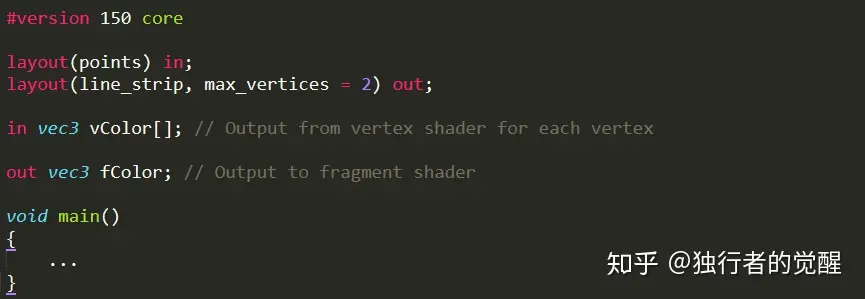
几何着色器
最终我们得到如下的结果,每个线段都有自己的颜色,而且与输入顶点的颜色相同。

几何着色器输出的图元带有颜色信息
几何着色器的应用
法线可视化
几何着色器的第一个应用是显示物体的法线,这对于光照效果的调试非常有帮助。我们首先在不使用几何着色器的情况下正常渲染一次场景;然后开启几何着色器第二次渲染场景,送到几何着色器的是三角形图元,我们为其每个顶点生成一个法线向量。
这里需要注意的是,几何着色器中使用的顶点坐标是经过顶点着色器变换后的裁剪空间坐标,所以传入到几何着色器的法线也需要变换到裁剪空间。我们这里需要知道法线向量的变换矩阵与顶点坐标的变换矩阵是不同的,需要使用矩阵的逆阵的转置来变换法向量,关于该矩阵的具体推导可以参考这个教程。顶点着色器如下所示,将法向量变换到裁剪空间。
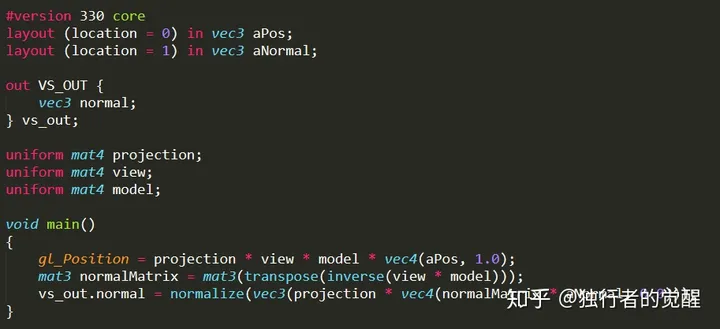
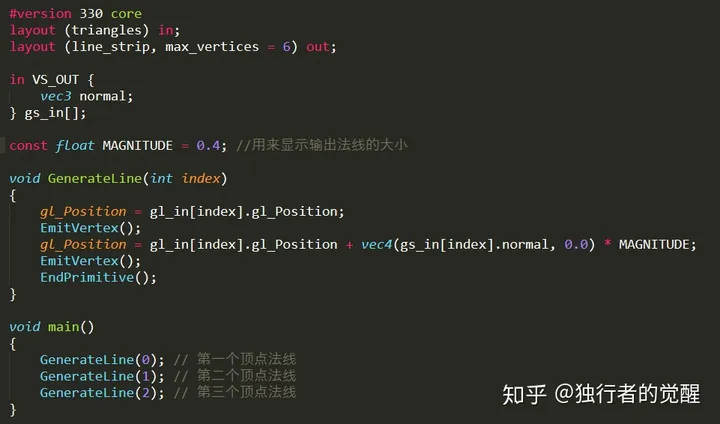
在几何着色器中,我们接受的输入图元是triangle,输出的图元是line_strip,我们这里输出的顶点数量max_vertices为6,因为我们需要为triangle的每个顶点输出法线,三个法线向量与三角形的法线相互平行。从下面的几何着色器中我们看到,这里为triangle每个顶点输出了两个顶点,分别是法线的起点和终点,用来表示法线。
最终我们可以得到如下的效果图,我们通过几何着色器来可视化茶壶和机器人的法线,我们注意到,这样的效果类似于给物体增加了毛发(Fur),所以几何着色器也经常用来实现毛发渲染。

茶壶法线可视化

机器人法线可视化
动态几何体形成 (Dynamically generating geometry)
接下来我们看下几何着色器的另一个应用:动态几何体形成。我们利用几何着色器可以实现物体的LOD技术 (Level of Detail)。比如,我们需要在游戏中绘制一个圆圈,那么我们可以根据距离摄像机的远近来调整圆圈的顶点数目,充分利用显卡的性能。我们首先来绘制一个十多边形 (10-sided polygon),这里需要使用到三角学的一些知识,如下图所示。
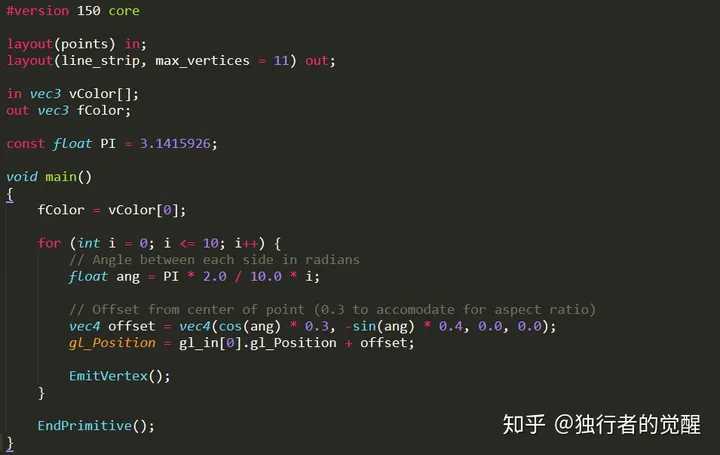
十多边形有十个顶点,这里我们绘制了十一个顶点,因为我们需要将多边形封闭起来,所以第一个顶点需要绘制两次。我们可到下面的结果:

具有不同顶点的多边形
接下来我们通过顶点数据来控制多边形的边数,也就是将边数变成顶点的一个属性值:

利用顶点的Sides数值来控制多边形的边数而不是原来的定值10,我们可以得到下面的效果图。四个多边形分别具有4、8、16和32条边。我们在游戏中可以根据玩家距离摄像机的远近来动态调整多边形边数这个属性值,实现LOD的效果。
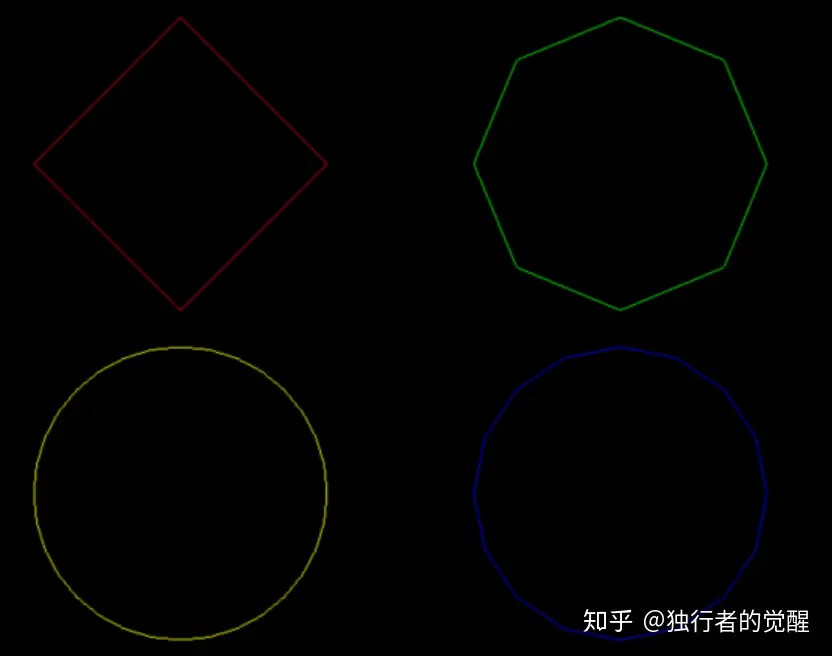
利用Sides变量控制多边形的显示
公告牌 (BillBoards)

公告牌技术就是以3D树木图片的四边形来代替3D树的渲染的技术。我们可以使公告牌总是面向摄像机,这样从远处看过去,公告牌不容易露出破绽,如上图所示。
假设y轴指向正上方,平面xz表示地面,则树木的公告牌立于xz平面切与y轴平行面向摄像机。下图是从y轴俯视看到的公告牌的坐标系。我们给定公告牌的中心位置C (我们可以根据几何着色器将该顶点扩展成四边形来展示公告牌),摄像机的位置E,通过叉乘我们可以得到公告牌局部坐标系和世界坐标系的对应关系:
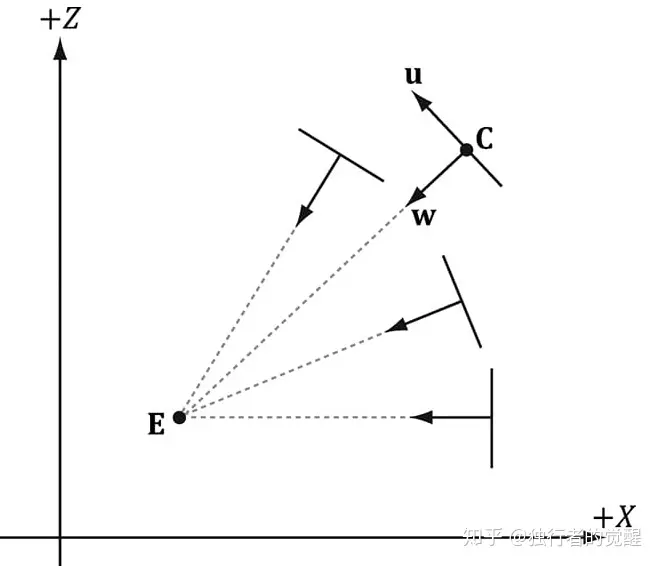
XZ平面的投影,摄像机和公告牌之间的位置信息
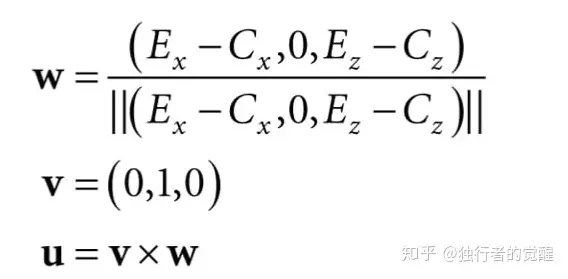
描述公告牌相对于世界坐标的坐标轴
通过公告牌的局部坐标系和世界坐标系之间的关系以及公告牌本身的大小,我们可以得到公告牌扩展后的四边形的四个顶点坐标如下:

四边形四个顶点坐标计算
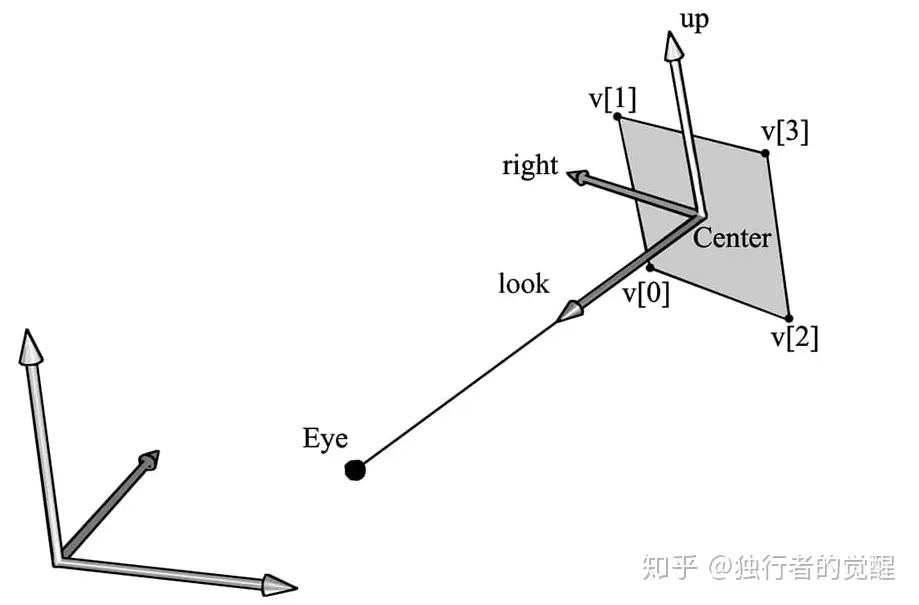
如何利用输入顶点得到四边形的四个顶点坐标示意图
我们输入几何着色器的正是公告牌的中心点Center,通过几何着色器来扩展为四边形进行展示。
Alpha-to-Coverage技术

我们在BillBoards技术中会根据树木的alpha值进行alpha测试,当我们靠近观察公告牌时,会发现裁剪树木留下的硬边缘问题,也就是俗称的锯齿问题。这个问题主要是由于discard()或clip()函数带来的,它们用来裁剪掉不需要树木纹理的像素,导致树木的边缘过渡不自然。
解决该问题的第一种方法是使用alpha-blending技术来代替alpha test。通过线性纹理过滤,我们可以使得公告牌边缘过渡更加自然。由不透明像素逐渐过渡到半透明像素,带来一种渐变的效果。但是,运用alpha-blending技术需要将场景中的物体按照从后往前的顺序进行排序和渲染。对于渲染一大片的森林或草原,排序带来的消耗将非常大。而且alpha-blending技术会在排序后带来大量的OverDraw问题,会很大影响程序的性能。


第二种方法是使用多重采样抗锯齿技术 (Multisampling Antialiasing,MSAA)。可以用来缓解多边形边缘的锯齿问题,使之更加平滑。该技术确实有效,不过也带来一些问题。开启MSAA技术后,硬件会生成多个样本 (Samples),根据样本的可见性和覆盖率来决定样本的颜色信息。关键在于,覆盖率是在多边形层次 (Polygon Level) 上确定下来的,所以MSAA技术并不会检查alpha通道,所以边缘过渡不会有不透明到半透明的过渡效果。如果想要在覆盖率计算过程中考虑alpha通道的情况,那就必须使用 Alpha-to-Coverage 的技术。Alpha-to-Coverage会使用纹理的alpha值来决定采样的覆盖率。
在开启了MSAA和alpha-to-coverage后,硬件会检测像素着色器返回的alpha值,并用于确定覆盖情况。比如本来利用MSAA得到的coverage是1,但是像素着色器返回的alpha为0.5,那么coverage变成了0.5,这样最后在resolve阶段,这个像素的颜色也被变淡了。正是通过这种技巧,将其颜色弱化,达到了柔软硬边的效果。关于alpha-to-coverage可以参考这篇文章。

当我们使用alpha测试来裁剪树叶或者围栏这类纹理时,建议使用MSAA和alpha-to-coverage技术来进行边缘过渡处理,所以我们发现其实alpha-to-coverage也属于抗锯齿技术的一种。
References
- https://medium.com/@bgolus/anti-aliased-alpha-test-the-esoteric-alpha-to-coverage-8b177335ae4f
- LearnOpenGL - Introduction
- Geometry shaders
编辑于 2019-08-12 13:07