685. 冗余连接 II

Problem: 685. 冗余连接 II

Reference

https://www.bilibili.com/video/BV1pr4y1U7u9

思路

在这里有下面四种情况

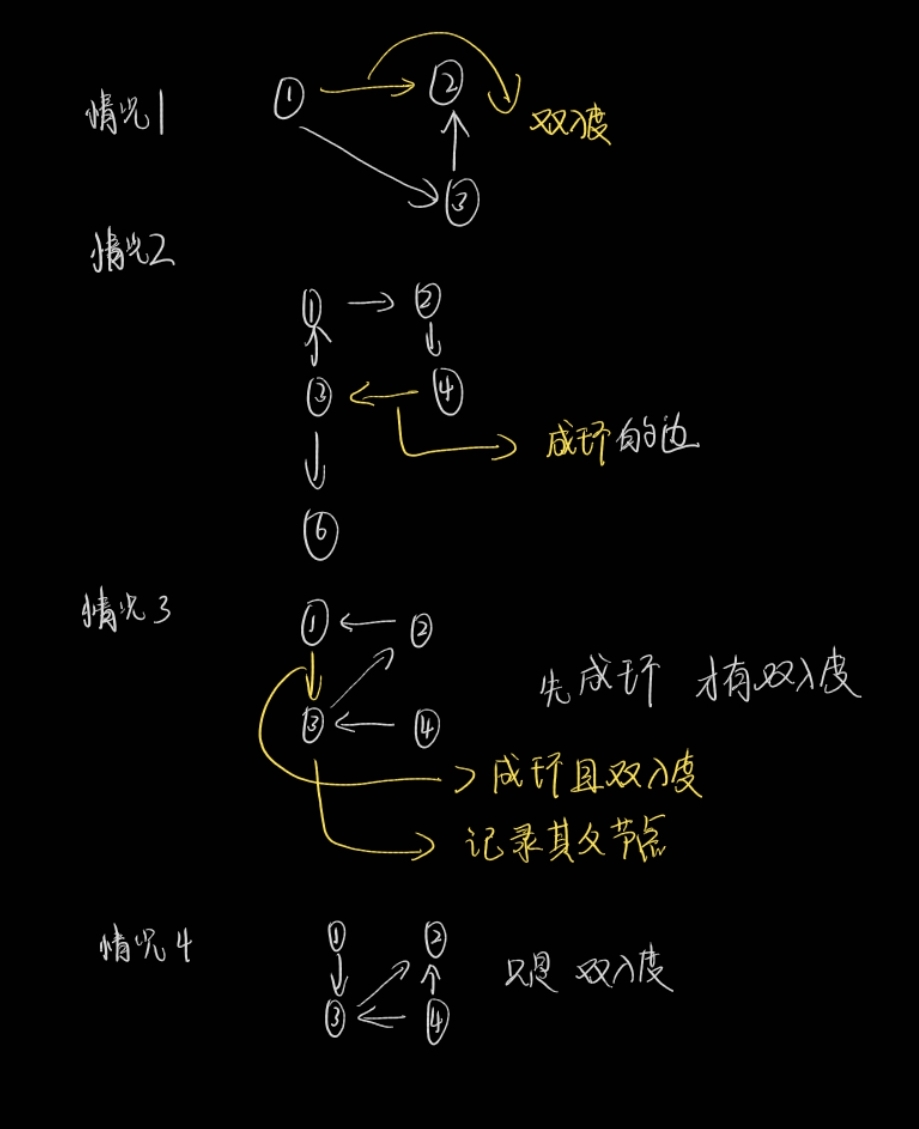
需要注意的是,第三种情况中一定是1->3这条边形成才有的4->3这条边,于是我们需要记录一个父节点数组,来记录各个点的父节点。

其他的看代码注释很容易看懂。

实在不明白,上面视频链接很清楚。

复杂度

时间复杂度:

添加时间复杂度, 示例： $O(n)$

空间复杂度:

添加空间复杂度, 示例： $O(n)$

Code

[]

class Solution {
public:
    vector<int> father;
    void init() {
        for (int i = 0; i < father.size(); i++) {
            father[i] = i;
        }
    }
    int find(int u) {
        if (father[u] == u)
            return u;
        return father[u] = find(father[u]);
    }
    void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v)
            return;
        father[v] = u;
    }
    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }
    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        // 获取顶点数量
        int len = edges.size();
        father = vector<int>(len+1,0);
        // 根据顶点数量创建并查集
        init();
        // 根据顶点数量创建parent数组，维护顶点父节点
        vector<int> parent(len + 1, 0);
        for (int i = 1; i <= len; i++) parent[i] = i;
        // 初始化双入度边及成环边的下标
        int doubleInd = -1, circleInd = -1;
        // 遍历输入数组
        for (int i = 0; i < len; i++) {
            int a = edges[i][0], b = edges[i][1];
            // 如果当前子节点已经被作为子节点连接过，则此时形成了双入度
            if (parent[b] != b) doubleInd = i;
            else {
                // 否则更新子节点的父节点
                parent[b] = a;
                // 如果两个顶点在同一个集合，则此时形成了环
                if (isSame(a,b)) circleInd = i;
                // 否则将子节点所在集合合并到父节点所在集合
                else join(a,b);
            }
        }
        // 如果当前只是成环的情况，返回成环的边
        if (doubleInd == -1) return edges[circleInd];
        // 如果只是双入度的情况，返回双入度的边
        if (circleInd == -1) return edges[doubleInd];
        // 如果是成环且双入度的情况，返回双入度子节点及其父节点组成的边
        int child = edges[doubleInd][1];
        return vector<int>{parent[child], child};
    }
};