Reference
1. 浅谈骨骼动画技术原理(一):基本介绍 - 知乎 (zhihu.com)
2. 浅谈骨骼动画技术原理(二):正向动力学 - 知乎 (zhihu.com)
3. 浅谈骨骼动画技术原理(三):逆向动力学 - 知乎 (zhihu.com)
4. 浅谈骨骼动画技术原理(四):蒙皮与其他技术 - 知乎 (zhihu.com)
作者: 启思
文章链接:如上
正文
第一篇 浅谈骨骼动画技术原理(一):基本介绍
人物模型是由三角面 mesh 组成的。为了让人物动起来,一个最简单的想法是直接修改 mesh 的各个顶点的坐标,这带来了几个问题:
- 逐顶点操作很容易带来非常不自然的结果
- 随着模型越来越精细,顶点越来越多,操作空间十分巨大
这加大了动画制作的难度。
可以在 mesh 中放置若干骨骼,骨骼的运动带动 mesh 的运动。这样,动画师只需要操作骨骼,就可以带动 mesh 完成动画的编辑。
与骨骼对应的,mesh 被称为皮肤(skin)
一段段骨骼之间相互连接,连接处称之为关节(joint)。骨骼可以绕着关节进行转动。
关节之间通过线段相连,可以形成一个树状结构,我们称之为关节模型:
工业界骨骼动画的制作流程
- 骨骼与标准姿势(T-pose)的绑定与蒙皮(binding, skinning)
- 动画师操作骨骼,制作关键帧(keyframe)
- 关键帧之间的插值形成整个动画
绑定与蒙皮:对于标准姿势,创建一套骨骼用来对应 mesh 上的顶点。这个对应做好了,才可以完成驱动操作。另外,这个对应好不好直接影响了动画的质量,这也是让万千美术头秃的工作
关键帧:这是制作动画的常用方法,通过指定关键的动作来表示动画
另一个角度上,可以这么理解:在关键帧编辑骨骼姿态,在非关键帧插值骨骼姿态,在所有帧上进行蒙皮。
插值
插值的目的是平滑连续。插值问题可以抽象成:给定 $f(0)=p_0$ ,$f(1)=p_1$,求 $f(t),0<t<1$
最简单的插值是线性插值,即 $f(t)=tp_0+(1-t)p1$
如果要求更高的平滑性的话,我们可以再取端点的若干阶导数值,如 Hermite Curve 插值,其插值公式是
$$f(t)=h_{00}(t)p_0+h_{10}(t)m_0+h_{01}p_1+h_{11}m_1$$
其中 $p_0,p_1$ 是端点值, $m_0,m_1$ 是端点导数值。四个参数如下计算
$$ℎ_{00}(t)=2t^3−3t^2+1$$
$$ℎ_{01}(t)=t^3−2t^2+t$$
$$ℎ_{10}(t)=−2t^3+3t^2$$
$$ℎ_{11}(t)=t^3−t^2$$
关于插值的更多内容,见 从零开始几何处理:函数拟合 - 知乎 (zhihu.com)
插值系数搞定了,现在我们考虑:已经有了关键帧的骨骼姿态,究竟要插值什么东西,才能得到非关键帧的骨骼姿态,并且让非关键帧动画平滑且连续?
一个非常简单的思路是,直接插值关节坐标。这在动作幅度小的时候问题不大,但是如果动作幅度大,不同的关节的运动速度是不同的,很容易插值出不自然的结果。
另一个方法是插值变换矩阵,这涉及了正向运动学的内容,我们留到第二篇文章解决。
还可以插值部分关节坐标,其余的对逐帧进行逆向运动学的解算,我们留到第三篇文章解决。
第二篇 浅谈骨骼动画技术原理(二):正向动力学
实际上,树上的每个关节节点存储的并不是它的绝对坐标,而是相对父节点的坐标,更精确的,是相对父节点的坐标变换矩阵。
由于存储的是相对变换,那么计算关节坐标和计算关节坐标到世界坐标的变换便不再是显然的。
正向运动学(Forward kinematics)正是为了解决这一问题:给定关节模型和每个节点相对父节点的变换矩阵,如何计算关节坐标到世界坐标的变换矩阵?
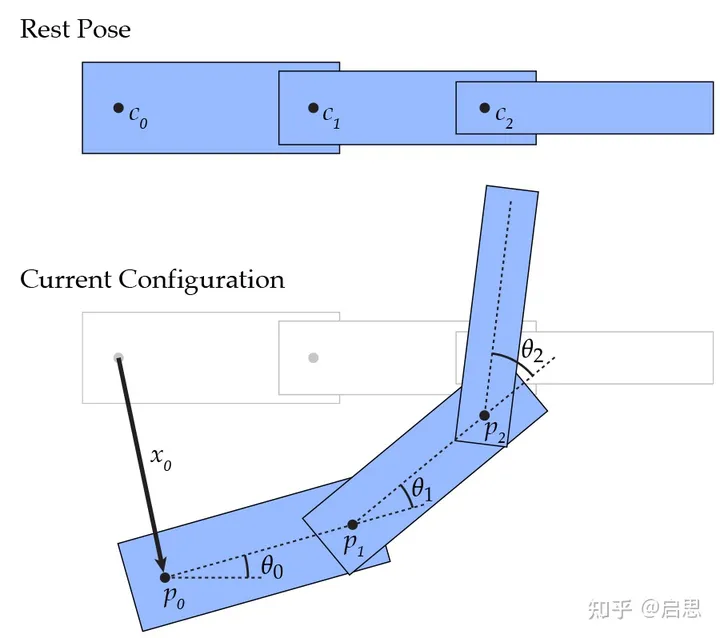
上图是三段骨骼。为了定义整个关节模型,我们需要储存:
- 每个关节所在骨骼的长度。
- 每个关节所在骨骼相对上一关节的旋转角度。
- 关节模型的根节点的坐标。
为了引入空间变换,首先介绍骨骼动画涉及的几个坐标空间(坐标系):
- 世界坐标系。顾名思义。树根的坐标代表了对应的物体在世界坐标系下的坐标。
- 关节坐标系。以某个关节为原点的坐标系,代表了树上某一节点的局部空间。
- 骨架(物体)坐标系。树根坐标为原点的坐标系。特别的,其实就是树根节点的关节坐标系。
正向运动学就是求解关节坐标系到世界坐标系的变换。
- 每个关节所在骨骼的长度:对应了当前关节坐标系到父关节坐标系的平移变换。
- 每个关节所在骨骼相对父关节的旋转角度:对应了当前关节坐标系到父关节坐标系的旋转变换。
- 关节模型的根节点的坐标:这对应了骨架坐标系到世界坐标系的平移变换。
正向运动学
回看上一张图。
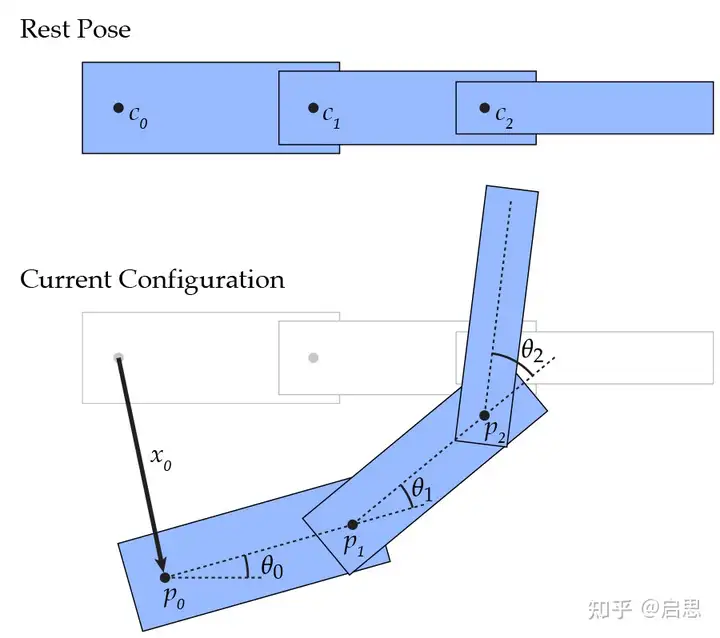
这里的根节点坐标是 $x_0$ 。定义关节的末端影响器为这个关节伸出去的末端。如何计算末端影响器的世界坐标?
设第 i 个关节对应的旋转矩阵是 $R_i$ ,平移矩阵是 $T_i$ ,原点坐标 $O$=(0,0,0) ,那么:
$p_0$ 的关节坐标是 $O$ ,这也是在骨架坐标系的坐标,通过根节点的世界坐标进行变换,即对应的世界坐标是 $x_0+O$
$p_1$ 的关节坐标是 $O$ ,首先由 $T_1$ 进行一个平移,再由 $R_1$ 进行旋转,得到它在父关节的关节坐标系坐标 $T_1R_1O$ ,这也是它在骨架坐标系的坐标,所以对应的世界坐标是$x_0+R_1T_1O$
$p_2$ 的关节坐标是 O ,同理可得它的世界坐标是 $x_0+R_1T_1R_2T_2O$
$p_3$ 同理,不过没在图上标注,就是最后一块骨骼的末端。世界坐标是$x_0+R_1T_1R_2T_2R_3T_3O$
如果我们把 x_0 也看做一个平移变换 T_0,再添加一个旋转变换 R_0=I,那么很容易发现,从只需要拿原点坐标乘平移、旋转矩阵,再乘父节点,一直乘到根节点,就可以得到关节的末端影响器的世界坐标。即
$$x_i=R_{root}T_{root}…R_{fa_i}T_{fa_i}R_iT_iO$$
所以,关节坐标系到世界坐标系的变换,就是根节点到该关节的变换矩阵之乘积。即
$$M_{i to world}=R_{root}T_{root}…R_{fa_i}T_{fa_i}R_iT_i$$
那么关节坐标系中任意点的坐标 � 在世界坐标系中的坐标 �(�) 为
$$p^{(w)}=M_{i to world}×p$$
另外注意到,我们可以通过树遍历一次性求出所有关节的变换矩阵
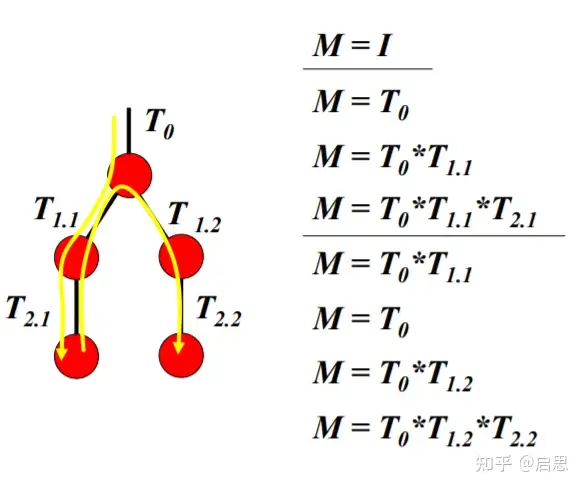
这里的 $T_i$ 实际上代表了刚刚的 $R_iT_i$ 。
由此,我们可以求解末端影响器的世界坐标,并且可以求解关节坐标系和世界坐标系任意点坐标之间的对应。此即正向动力学。
第三篇 浅谈骨骼动画技术原理(三):逆向动力学逆向运动学
上一篇文章(**浅谈骨骼动画技术原理(二):正向动力学 - 知乎 (zhihu.com)**)中,我们介绍了如何通过关节模型来计算末端影响器的位置。
更具体的,假设每块骨骼的长度不变,我们可以通过旋转骨骼来改变关节末端影响器的坐标,即 $x=f(\theta)$ ,此为正向运动学。
逆向运动学(Inverse kinematics)是求解相反的问题:给定末端影响器坐标,计算旋转的角度,即 $\theta=f^{-1}(x)$
逆向运动学的需求十分常见,例如需要手去抓取物品。如果通过不断调节旋转角度来达成,那么会非常麻烦。
有了逆向运动学,编辑关键帧会变的比较轻松。另外,对于插值非关键帧,我们也可以对关节坐标进行插值,然后对每一个非关键帧进行逆向运动学求解,这样的结果可能更加自然。
但是,求解逆向运动学是比较困难的:
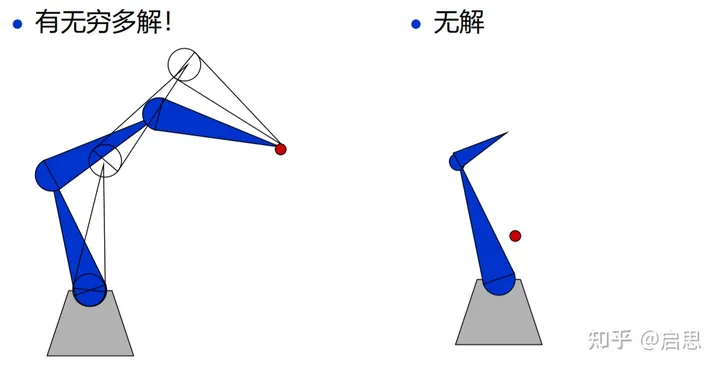
循环坐标下降法(CCD)
循环坐标下降法(CCD, Cyclic Coordinate Descent)是一种启发式的 IK 算法,也是目前游戏中求解 IK 的标配算法。算法思路非常简单:
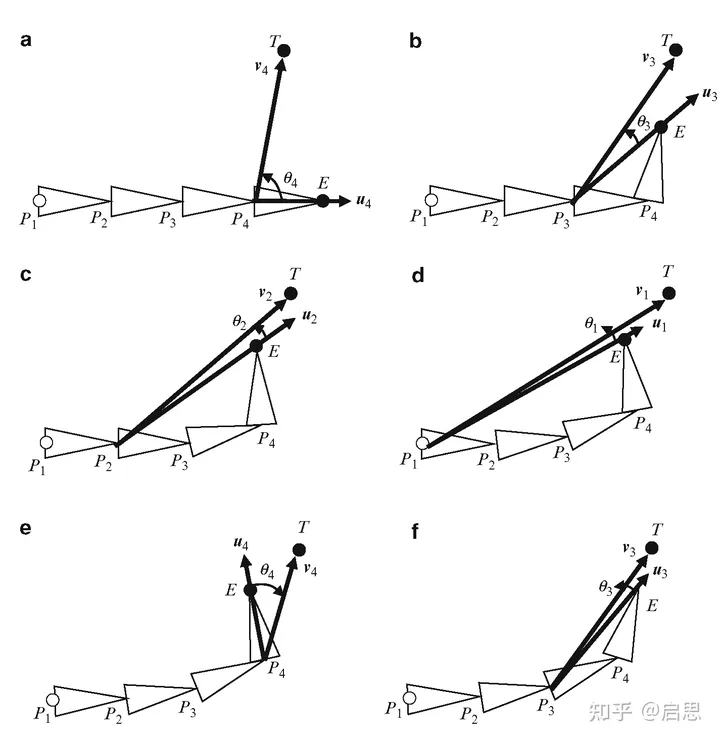
如上图所示,就是每次选择某一个关节旋转一个角度,让末端影响器距离目标点位置更近。通过多次循环选择关节,最终得到结果。
具体来说,就是每次旋转到当前关节与目标点的连线上。
每次将末端关节旋转到目标与下一个节点的连线上,到达最后一个节点就从新开始做之前的操作
这个方法是可以收敛的,其实就是一种经典的优化方法,叫坐标下降法,每次只优化一个坐标,多次优化达到目的。