Reference
NavMesh背后的实现原理 - 知乎 (zhihu.com) 这篇文章主要是讲体素化
Navigation Mesh寻路算法 - 知乎 (zhihu.com)NavMesh的寻路原理
几何寻路:漏斗算法(Funnel Algorithm)-CSDN博客网格寻路的漏斗算法
正文
NavMesh 过程:
1.体素化 得到寻路所需的信息 比如是否能够行走 高度等等
一般来说,找到一个游戏角色的最佳路径至少需要3个阶段。在第一阶段,游戏世界被转换成几何表示,例如导航网格
$A^*$也是网格不过不是Mesh网格而是方格
2.$A^*$寻路 找到对应多边形
先将多边形寻路抽象为一张图($G^{‘}$),原理是将多边形中心互相连接
使用$A^*$在$G^{‘}$上寻路,找到这个路径所在的多边形
在阶段2,在这样的网格中执行$A^*$搜索。因为$A^*$搜索不能给出真实路径(详见第4.1节),所以需要进一步的过程来找到真实路径,
你看下面标出红色的路径就是不正确的路径,因为黑色的是不可通过的,但是使用$A^*$只能得到直线路径
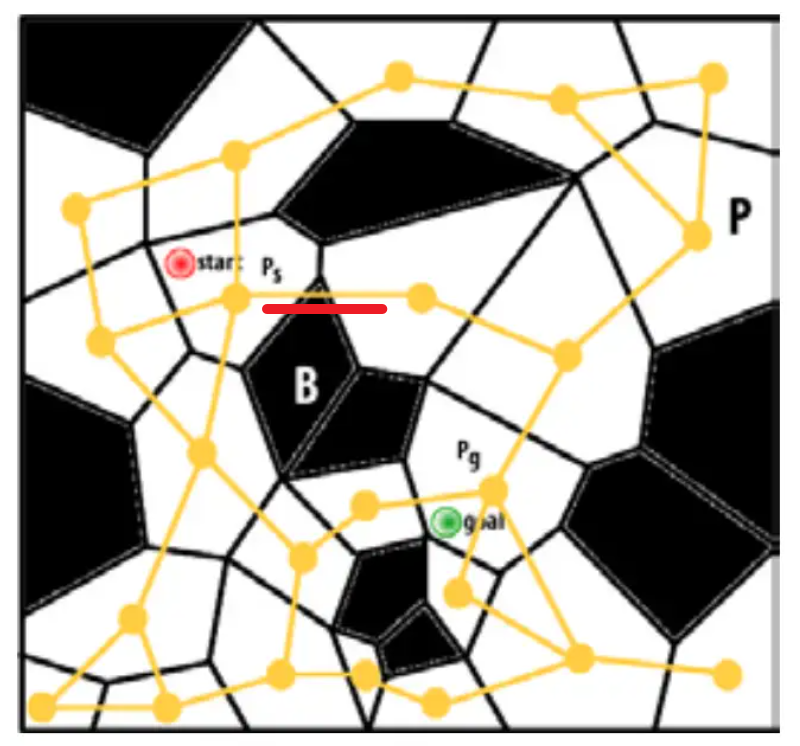
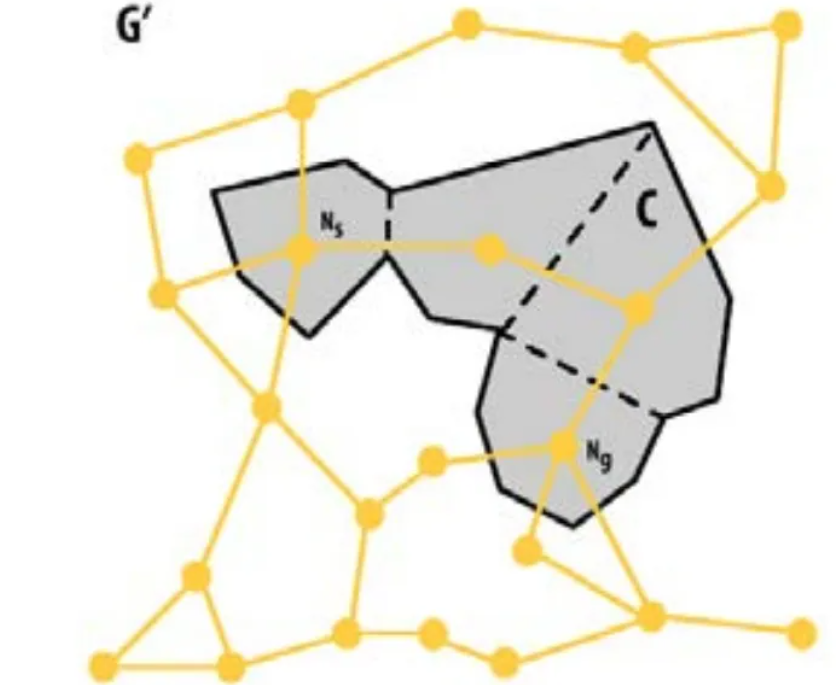
首先,我们必须找到一组多边形 ⊆ ,一个最佳路径将通过。如果Ps是起点所在的多边形,那么Ps一定是C中的第一个多边形,如果Pg是目标所在的多边形,那么Pg一定是C中的最后一个多边形,要找到C的剩余部分,我们必须在地图中做一些改变。G中的每个多边形映射到G ‘中的一个节点。例如,Ps映射到NSA,Pg映射到Ng。如图2所示,G中两个多边形共享的每条边被映射到连接G’中两个节点的边。
意思就是找到对应的$A^*$路径上的多边形
3.将多边形三角形剖分 使用漏斗算法寻路
三角剖分是NavMesh的一种特殊情况,其中多边形被替换为三角形。三角形的最小角必须最大化。这一特性保证了最佳路径不会与任何三角形交叉超过一次。在三角测量中,单独使用$A^*$不能产生真正的路径,而是给出一组有起点和终点的三角形。在形成的路径中,一个以起点和终点为两个节点的简单多边形描绘了中间三角形的周长,
对于一个点目标,这种路径可以用漏斗算法在线性时间内找到。在这里,我们不描述原始的漏斗算法,而是更愿意给出一个简化的版本,简单愚蠢的漏斗算法(SSF),它是由Mononen在2010年首次提出的。
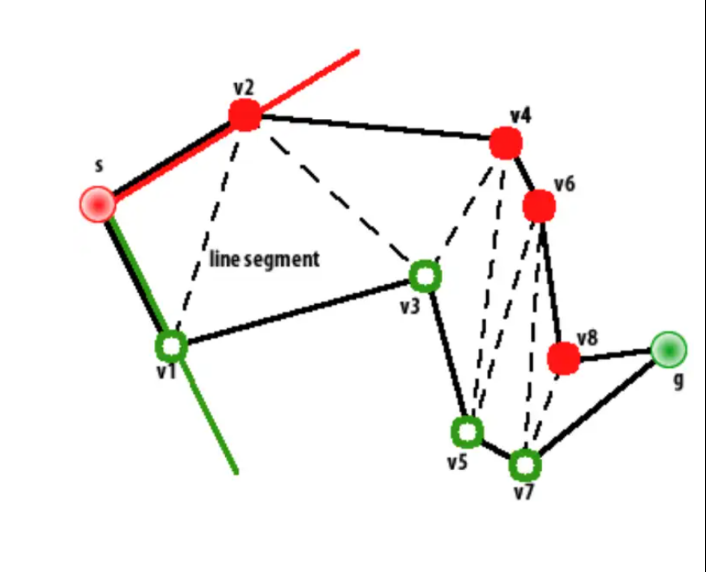
现在只只关注这几个多边形,我们使用漏斗算法进行寻路,漏斗算法就是一个漏斗不断缩小的过程,
贪婪的方向是小漏斗 漏斗变为负数或者0 进入到下一个节点
当漏斗缩小为0或者负时,更新漏斗顶点
luo